) and (2), to find the equation of the line, y = mx b, that passes through the points y2y, first, she used the definition of slope and determined that the value of mis x, given this information, which expression must represent the value of b?The equation of the parabola whose graph is given above is y = (x 1)(x − 2) = x2 − x − 2 Example 2 Graph of parabola given vertex and a point Find the equation of the parabola whose graphThe "general" form of a parabola's equation is the one you're used to, y = ax 2 bx c — unless the quadratic is "sideways", in which case the equation will look something like x = ay 2 by c The important difference in the two equations is in which variable is squared for regular (vertical) parabolas, the x part is squared;
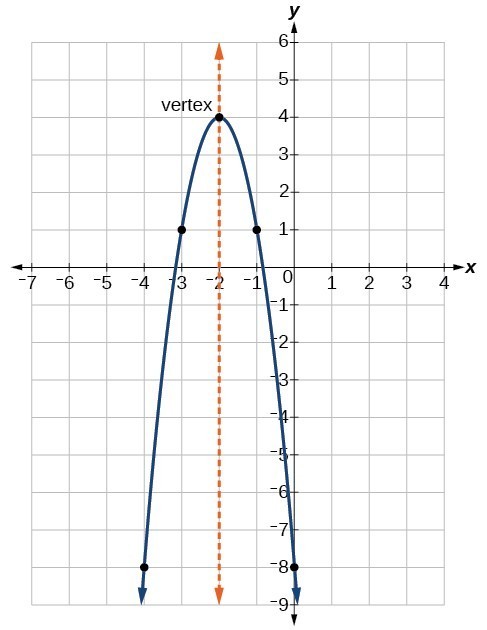
Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
Graph the parabola y=x^2-4x+5
Graph the parabola y=x^2-4x+5-None 10 x y 2 4 6 8Vertex Showing top 8 worksheets in the category – Graphs Of Parabolas 6 2 Axis of Sym Graphing Parabolas Worksheet Algebra 1 Ax2 bx c 0 Now we will look at graphs of the standard form of quadratic equations X 5 Opens Translating Parabolas 12Graph the equations ATextbook solution for Precalculus Mathematics for Calculus 6th Edition 6th Edition Stewart Chapter 111 Problem 28E We have stepbystep solutions for




Graphing Quadratic Functions A Quadratic Function Is An Equation Of The Form Y Ax 2 Bx C Ppt Download
The beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetryParabolas A parabola is the graph of a quadratic polynomial in one variable (see more in the Polynomials section) Its general equation comes in three forms \begin{array}{l l} \text{Standard form } & y = ax^2 bx c \\ \text{Vertex form } & y = a(xh)^2 k \\ \text{Factored form } & y = a(xr)(xs) \end{array} The factored form of theFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience
Howto Graph Horizontal Parabolas \left (y=a x^ {2}b xc or f (x)=a (xh)^ {2}k\right) using Properties Step 1 Determine whether the parabola opens to the left or to the right Step 2 Find the axis of symmetry Step 3 Find the vertex Step 4 Find the x interceptEach parabola is, in some form, a graph of a seconddegree function and has many properties that are worthy of examination Let's begin by looking at the standard form for the equation of a parabola The standard form is (x h) 2 = 4p (y k), where the focus is (h, k p) and For a quadratic of the form #x = ay^2 by c#, the axis is a line that passes through the vertex and is parallel to the #y# axis For our parabola, the axis is the line #y = 2 It's not part of the parabola itself, but lightly marking this line on your graph can help you see how the parabola curves symmetrically Step 5 Calculate and plot the #x#intercept #x= y^2 4y 3 = (0)^2
Change a, Change the Graph Another form of the quadratic function is y = ax 2 c, where a≠ 0 In the parent function, y = x2, a = 1 (because the coefficient of x is 1) When the a is no longer 1, the parabola will open wider, open more narrow, or flip 180 degrees Examples of Quadratic Functions where a ≠ 1The standard equation of a parabola is (x−h)2 = 4p(y−k) ( x − h) 2 = 4 p ( y − k) where (h,k) ( h, k) is the vertex 4p 4 p is the length of the latus rectum Note that the squared willGraphing y = (x h)2 k In the graph of y = x2, the point (0, 0) is called the vertex The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y
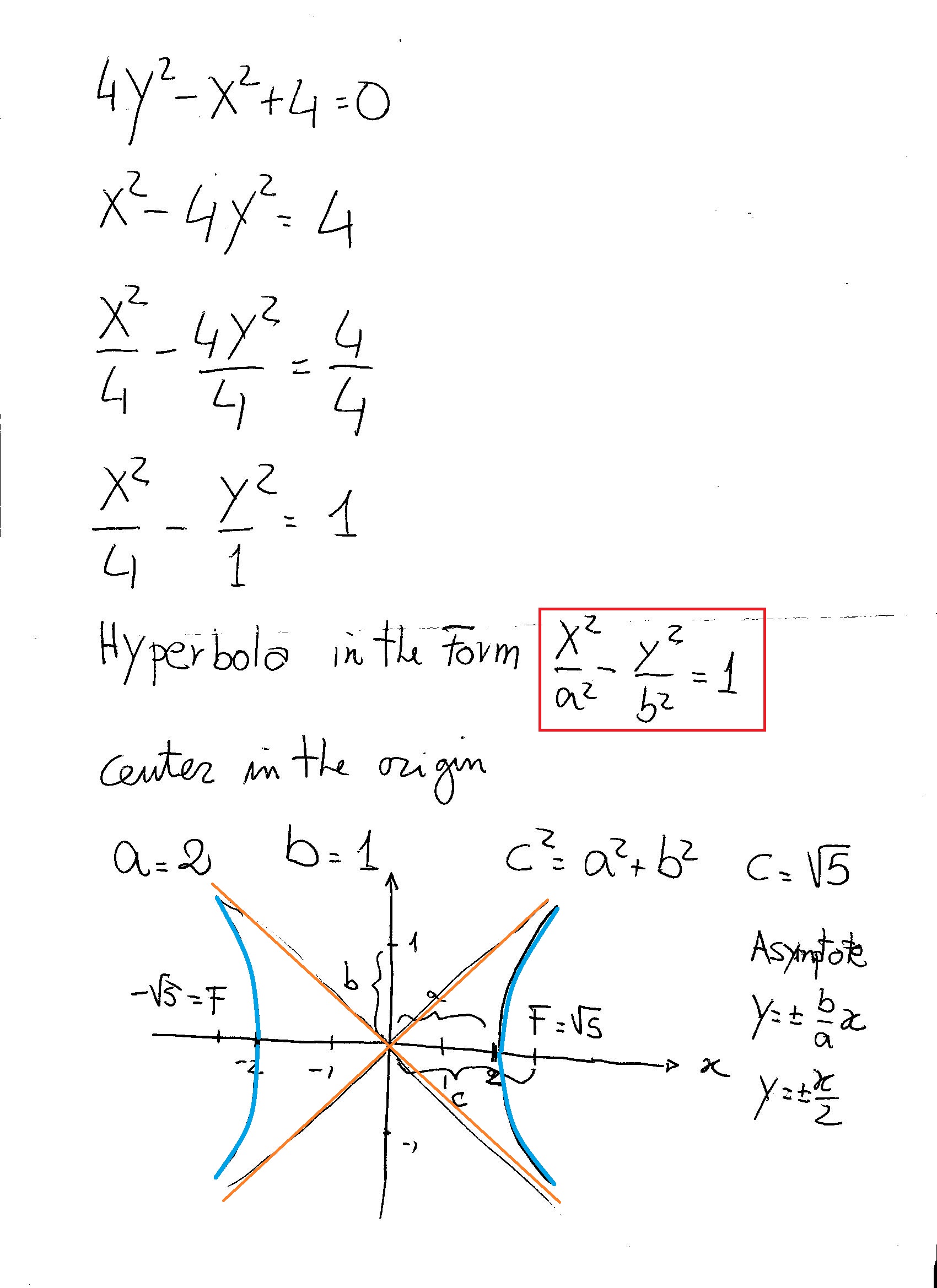



How Do You Identity If The Equation 4y 2 X 2 4 0 Is A Parabola Circle Ellipse Or Hyperbola And How Do You Graph It Socratic




Parabola X Y 2 Graph Novocom Top
IXL Graph parabolas (Algebra 2 practice) Graphing Parabolas Part 2 Graph these and remember to identify what's going on and not by plotting points Label 5 points!The graph of any quadratic equation y = a x 2 b x c, where a, b, and c are real numbers and a ≠ 0, is called a parabola When graphing parabolas, find the vertex and yintercept If the xintercepts exist, find those as well Also, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 aGraph the parabola, y =x^21 by finding the turning point and using a table to find values for x and y



Graphs Of Equations



Solution Graph The Parabola Y X 4 2 2
4 • the two points ( a , b ) and (− a , b ) are equidistant from the yMore y = a (xh)^2 k is the vertex form equation Now expand the square and simplify You should get y = a (x^2 2hx h^2) k Multiply by the coefficient of a and get y = ax^2 2ahx ah^2 k This is standard form of a quadratic equation, with the normal a, b and c in ax^2 bx c equaling a, 2ah and ah^2 k, respectivelyAs you indicated the parabola x = y 2 is "on its side" x = y 2 You can determine the shape of x = 4 y 2 by substituting some numbers as you suggest Sometimes you can see what happens without using specific points Suppose the curves are x = y 2 and x = 4 y 2 and and you want to find points on the two curves with the same yvalue Then




Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra



What Is The Graph Of Y2 2y X Quora
Like the ellipse and hyperbola, the parabola can also be defined by a set of points in the coordinate planeA parabola is the set of all pointslatex\,\left(x,y\right)/latex in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrixIn maths, the graph of any quadratic equation is in the parabola shape Thus, the graph for parabolic or quadratic equation can be drawn using the coordinates that satisfies the given equation or the roots of the given equation In general, the parabolic equation is written as y = ax 2 bx c Also, a parabola is a plane curve and is approximately U – ShapedTextbook solution for Precalculus Mathematics for Calculus (Standalone 7th Edition James Stewart Chapter 111 Problem 30E We have stepbystep solutions for your textbooks written by Bartleby experts!
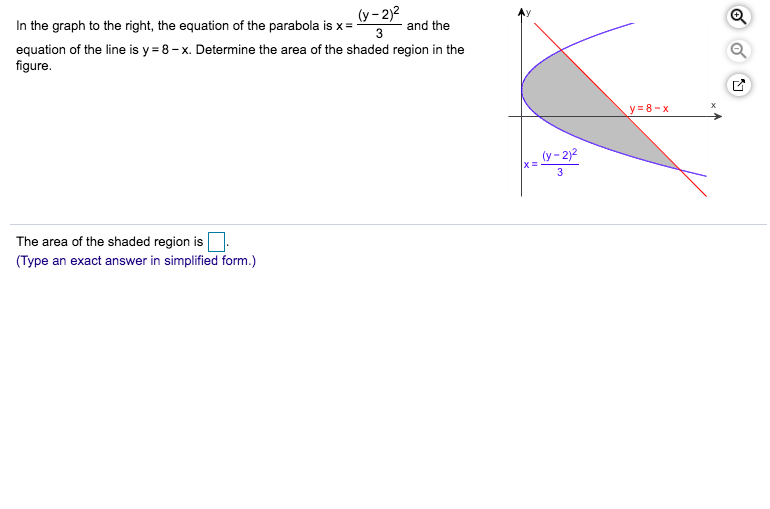



In The Graph To The Right The Equation Of The Chegg Com



8 5 Graphing Quadratic Equations Ase Algebra For Adult Education Openstax Cnx
The most general form of a quadratic function is, f (x) = ax2 bx c f ( x) = a x 2 b x c The graphs of quadratic functions are called parabolas Here are some examples of parabolas All parabolas are vaguely "U" shaped and they will have a highest or lowest point that is called the vertexIn standard form the equation of this parabola would be y = 05(x1)2 – 3 or y = (1/2)*(x – 1)^2 – 3 as it would be written for a computer 1 Open Microsoft Excel In cell A1, type this text Graph of y = 05(x1)2 – 3 You may enter the general form of the equation if you wish instead of the standard form Remember to make the numberOne graph has the point (4,2) plotted in which the parabola passes through (Ushaped parabola right side up) The vertex is at (3,0) and the parabola does not pre cal What is the center of the conic whose equation is x^2 2y^2 6x 8y = 0 2Which one




Graph Quadratic Functions Using Properties Intermediate Algebra




Solution For The Parabola Y X 2 36 Graph Of A Parabola Opening Down At The Vertex 0 36 Crossing The X Axis At 6 0 And 6 0
I do not know how to graph the parabola y= x^2 Plot a few points and draw a smooth curve thru themWe're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2, where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0 Let's vary the value of a to determine how the graph changesA quadratic function in the form f (x) = ax2 bxx f ( x) = a x 2 b x x is in standard form Regardless of the format, the graph of a quadratic function is a parabola The graph of y=x2−4x3 y = x 2 − 4 x 3 The graph of any quadratic equation is always a parabola




6 2 Graphing Parabolas Function Language And Graphing With A Table Ppt Video Online Download




Parabola X Y 2 Graph Novocom Top
It's a horizontal shift! The plot can be obtained by reflecting the function y=x^2/2 about the 45degree line All the previous answers (PSTricks, MetaPost, TikZ) use a plot to draw the parabola So they use a lot of segments to approximate it In the spirit of this answer I want to advocate to use a single quadratic (cubic) curve to draw the exact parabolaGraph x=y^2 x = −y2 x = y 2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for − y 2 y 2 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c
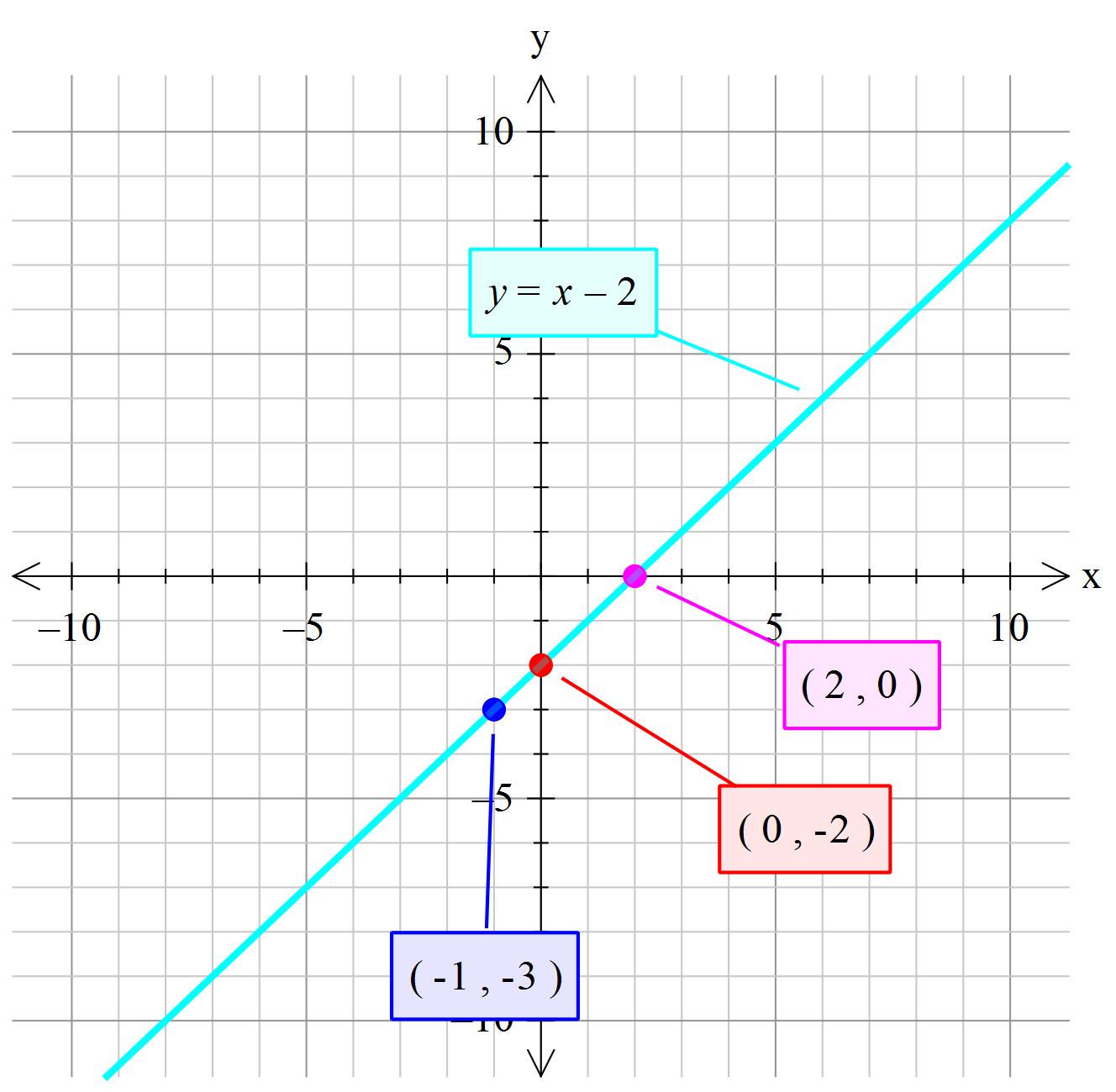



How Do You Graph The Line X Y 2 Socratic
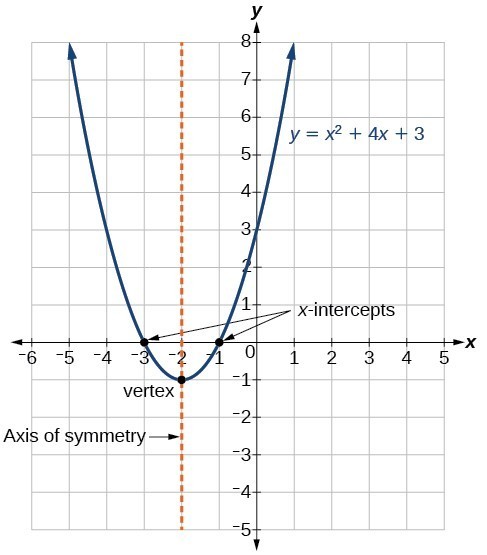



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
If the coefficient of the x 2 term is negative, the vertex will be the highest point on the graph, the point at the top of the " U "shape The standard equation of a parabola is y = a x 2 b x c But the equation for a parabola can also be written in "vertex form"Answers Click here to see ALL problems on Rationalfunctions Question 444 graph the parabola y= (x5)^2 4 Answer by venugopalramana (3286) ( Show Source ) You can put this solution on YOUR website!How to Graph a Parabola of the Form {eq}y=x^2 bx c {/eq} Example 1 Our quadratic equation is {eq}y = x^2 2x 3 {/eq} Step 1 First we need to find the vertex of our parabola
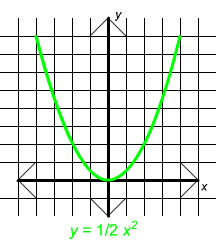



Parabolas And Cubics




What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora
How to Graph a Parabola with no xintercepts y = x^2 2 Here we're asked to graph a quadratic function, the first step is to determine the y intercept the y intercept occurs when x is 0 so when x is 0 here y you can easily see should be 2 the next step is to determine the xintercepts in this case you find the xintercepts when y is equal to 0 so 0 equals x squared plus 2 subtracting 2Parabola Opens Right Standard equation of a parabola that opens right and symmetric about xaxis with vertex at origin y 2 = 4ax Standard equation of a parabola that opens up and symmetric about xaxis with at vertex (h, k) (y k) 2 = 4a(x h) Graph of y 2 = 4axGraph the parabola y= (x5)^2 4




Answered In The Graph To The Right The Equation Bartleby



Transformations Of Equations Of Parabola Parametric Equations Of Parabola
Graph y^2=2x y2 = 2x y 2 = 2 x Rewrite the equation as 2x = y2 2 x = y 2 2x = y2 2 x = y 2 Divide each term by 2 2 and simplify Tap for more steps Divide each term in 2 x = y 2 2 x = y 2 by 2 2 2 x 2 = y 2 2 2 x 2 = y 2 2 Cancel the common factor of 2 2The parabola equation can also be represented using the vertex form The vertex form of the parabola equation is represented by f(x) = y = a (xh) 2 k Here, (h, k) is the vertex point of the parabola Similar to the standard form of the parabola equation, the orientation of the parabola in the vertex form is determined by the parameter "a"The graph of mathy^2=ax/math will be parabola Two graphs are shown below for positive and negative values of matha=1/math matha=1/math matha=1/math



Exploration Of Parabolas




X Y 4 X Y 2 Graph Novocom Top
When graphing, we want to include certain special points in the graph The yintercept is the point where the graph intersects the yaxisThe xintercepts are the points where the graph intersects the xaxisThe vertex is the point that defines the minimum or maximum of the graphAnd shift it horizontally to that spot *I always remember that, if the extra thing is inside with the x, then if affects x values these move itGraph horizontal parabolas (x = a y 2 b y c or x = a (y − k) 2 h) (x = a y 2 b y c or x = a (y − k) 2 h) using properties Step 1 Determine whether the parabola opens to the left or to the right Step 2 Find the axis of symmetry Step 3 Find the vertex Step 4 Find the xintercept Find the point symmetric to the xintercept



Quadratics Graphing Parabolas Sparknotes




Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube
Here are the steps required for Graphing Parabolas in the Form y = a (x – h) 2 k Step 1 Find the vertex Since the equation is in vertex form, the vertex will be at the point (h, k) Step 2 Find the yintercept To find the yintercept let x = 0 and solve for y Step 3 Find the xintercept (s)And y = −√ x (the bottom half of the parabola)Question I do not know how to graph the parabola y= x^2 Found 2 solutions by stanbon, jim_thompson5910 Answer by stanbon(757) (Show Source) You can put this solution on YOUR website!




In The Graph To The Right The Equation Of The Chegg Com
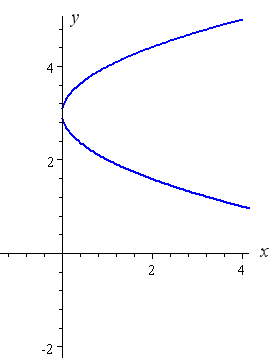



How To Draw Y 2 X 2
Lindsay used two points, (x, y; The curve y 2 = x represents a parabola rotated 90° to the right We actually have 2 functions, y = √ x (the top half of the parabola);Graph each parabola y=(x4)^{2}1 Boost your resume with certification as an expert in up to 15 unique STEM subjects this summer




Content Transformations Of The Parabola
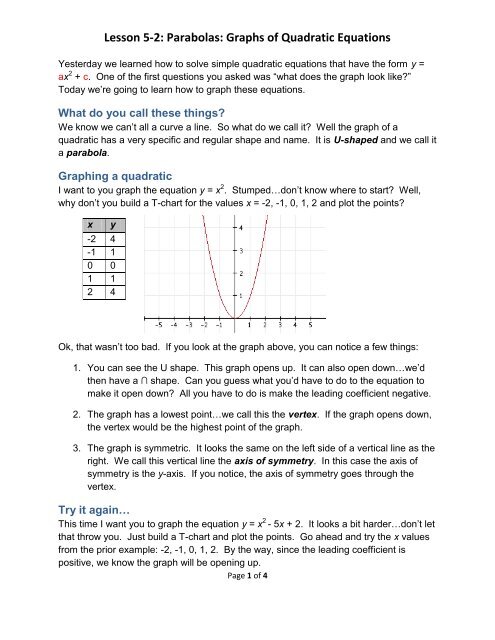



Lesson 5 2 Parabolas Graphs Of Quadratic Equations
Axis\ (y2)=3 (x5)^2 axis\3x^22x5y6=0 axis\x=y^2 axis\ (y3)^2=8 (x5) axis\ (x3)^2= (y1) parabolafunctionaxiscalculator axis x=y^2 enX 2 = 4py The graph of the parabola would be the reflection, across the x axis of the parabola in the picture above A way to describe this is if p > 0, the parabola "opens up" and if p 0 the parabola "opens down"Parabolas can have both xintercepts and y intercepts yintercept As you can see from the picture below, the yintercept is the point at which the parabola intercepts the yaxis xintercepts The xintercepts are the points or the point at which the parabola intersects the xaxis A parabola can have either 2,1 or zero real x intercepts
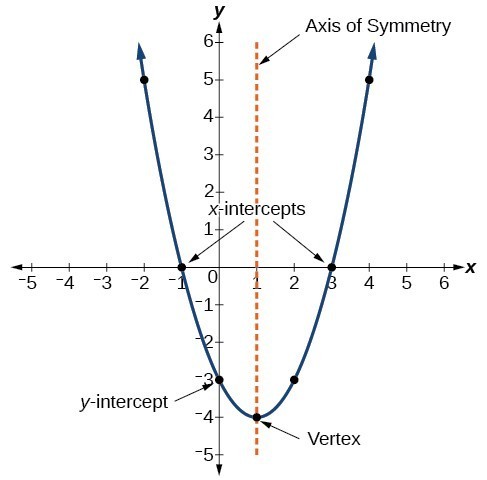



Characteristics Of Parabolas College Algebra




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
The graph is a parabola If ( a , b ) is a point belonging to the parabola, that is 8 b = a 2 , then (− a , b ) also belongs to the parabola since b = (− a ) 2 Note that 6 • the line segment joining ( a , b ) and (− a , b ) is perpendicular to the y axis;Parabola The standard form equation of a general quadratic (polynomial functions of degree 2) function is f(x) = ax 2 bx c where a ≠ 0 If b = 0, the quadratic function has the form f(x) = ax 2 c Since f(x) = a(x) 2 c = ax 2 c = f(x), Such quadratic functions are even functions, which means that the yaxis is a line of symmetry of the graph of f



How Would The Area Between X Y 2 A 2 A X And Y 2 A X A 2 X Be Found Quora



Find The Vertex Focus And Directrix Of The Chegg Com




Parabola X Y 2 Graph Novocom Top
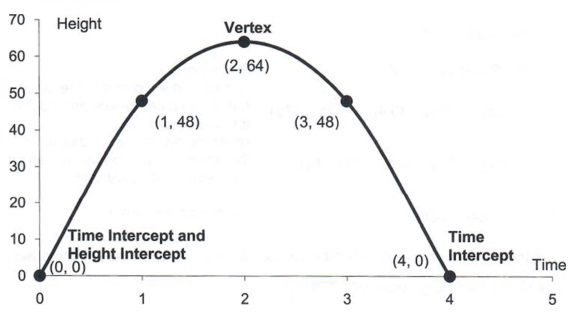



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2




Graph Of An Equation




Graphing Quadratic Functions Lesson Article Khan Academy
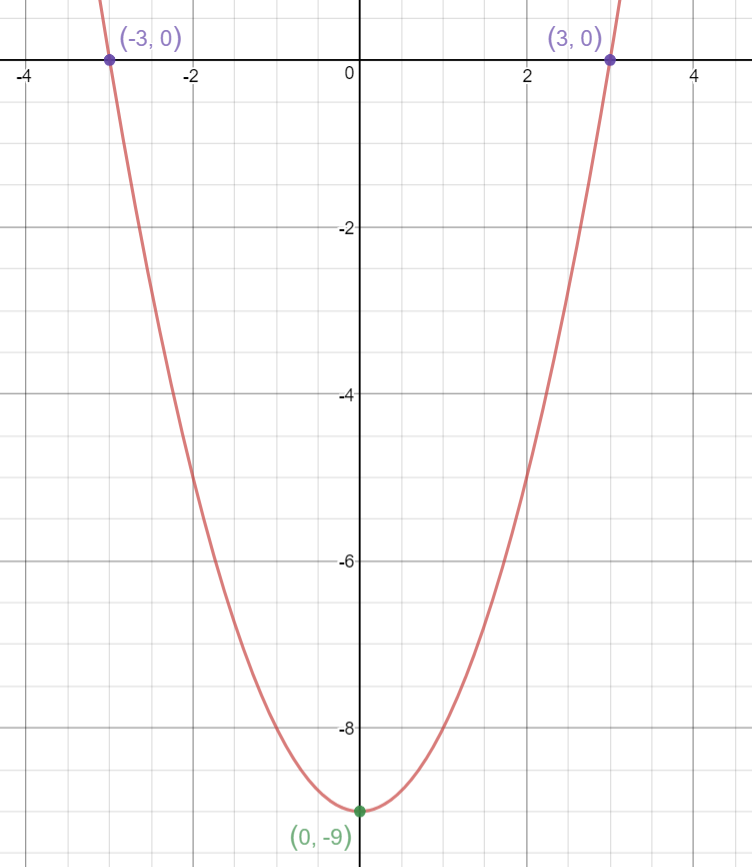



How Do You Graph Y X 2 9 Socratic




Quadratic Function




What Does X Y 2 Look Like On A Graph Study Com




Rough Sketch Of The Circle X 2 Y 2 8x And The Parabola Y 2 4x Mathematics Stack Exchange




Content Transformations Of The Parabola




Quadratic Function




How To Draw Y 2 X 2
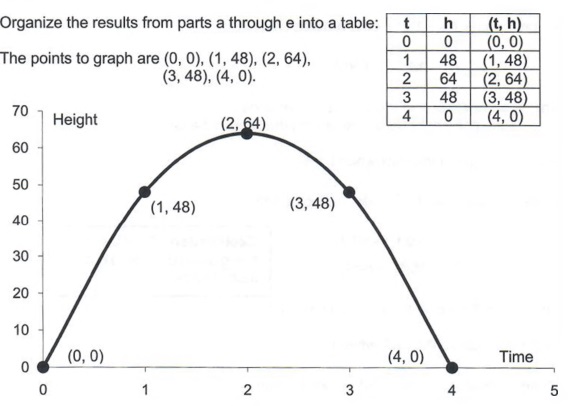



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver



Parabolas




Graphing Quadratic Functions A Quadratic Function Is An Equation Of The Form Y Ax 2 Bx C Ppt Download



1




Evaluating Area Between Two Curves X 4 Y 2 And X Y 2 For Dx And Dy Mathematics Stack Exchange




Use The Graph To Write An Equation For The Parabola A Y X 2 5 B Y X 2 25 C Y 5x 2 D Y Brainly Com



Quadratics Graphing Parabolas Sparknotes




Graph Of Xy 2 Novocom Top



Xy 1




Parabola X Y 2 Graph Novocom Top



8 5 Graphing Quadratic Equations Ase Algebra For Adult Education Openstax Cnx



Find The Area Of The Region Included Between The Parabola Y2 X And The Line X Y 2 Quora




Parabola The Set Of All Points That Are Equidistant From A Given Point Focus And A Given Line Directrix Ppt Download




Find The Area Bounded By The Parabola Y 2 X 2 And The Straight Line Y X 0 Youtube




In The Graph To The Right The Equation Of The Chegg Com



How Do You Sketch The Graph Of Y X 2 8 And Describe The Transformation Socratic
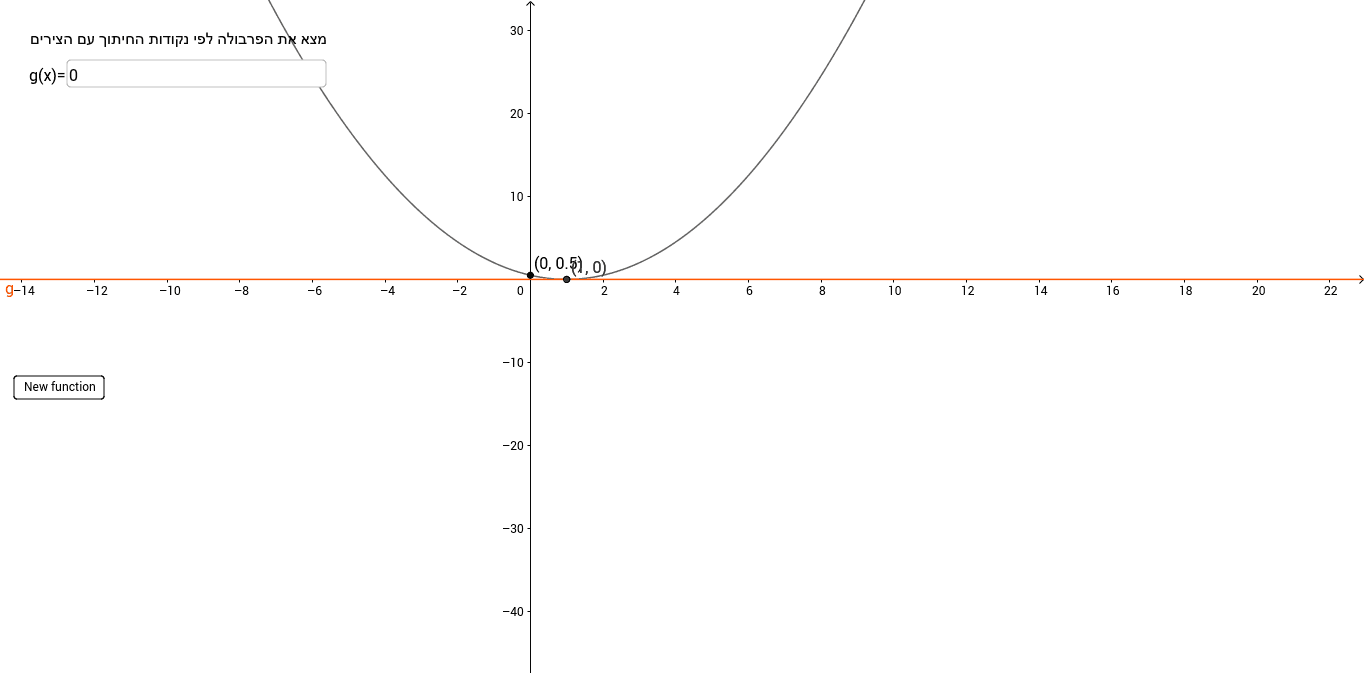



Parabola Match Graph To Function X Y Intersection Points Geogebra




Graph A Parabola In Vertex Form Using A Table Of Values Part 1 Youtube
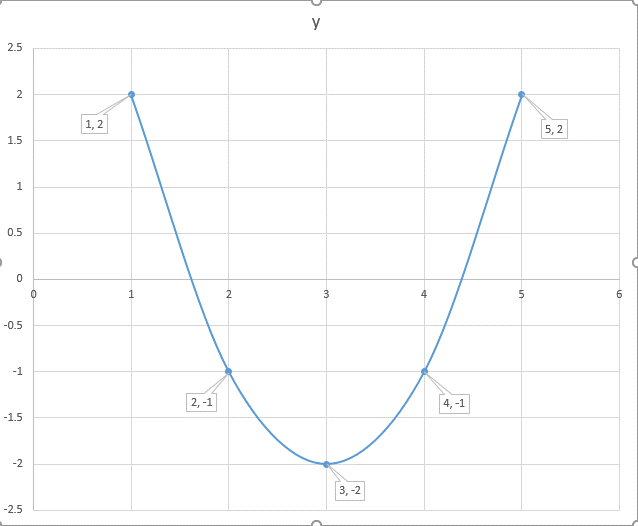



How Do You Graph The Parabola Y X 3 2 2 Using Vertex Intercepts And Additional Points Socratic
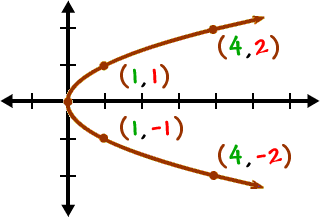



Sideways Parabolas 1
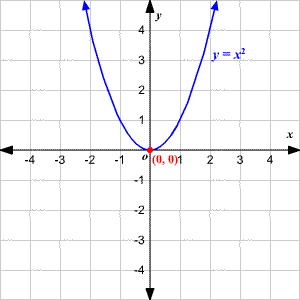



Parabolas



Solution Graph The Parabola Y 3 2 X 2




How To Graph Y X 2 1 Youtube




Graph Both Functions To Find The Solution S To The System F X X 1 G X X2 6x 7 Use The Line Brainly Com




Graph Y X 2 3 Youtube



Solution How To Graph X Y 2 6y 8 This Is Parabola




Find The Area Of The Region In The Xy Plane Enclosed By Two Parabolas Y X 2 And Y 2x X 2 Socratic



Quadratics Graphing Parabolas Sparknotes




In The Xy Plane The Graph Of The Function Q Has A Parabola The Graph Intersects The X Axis At Brainly Com
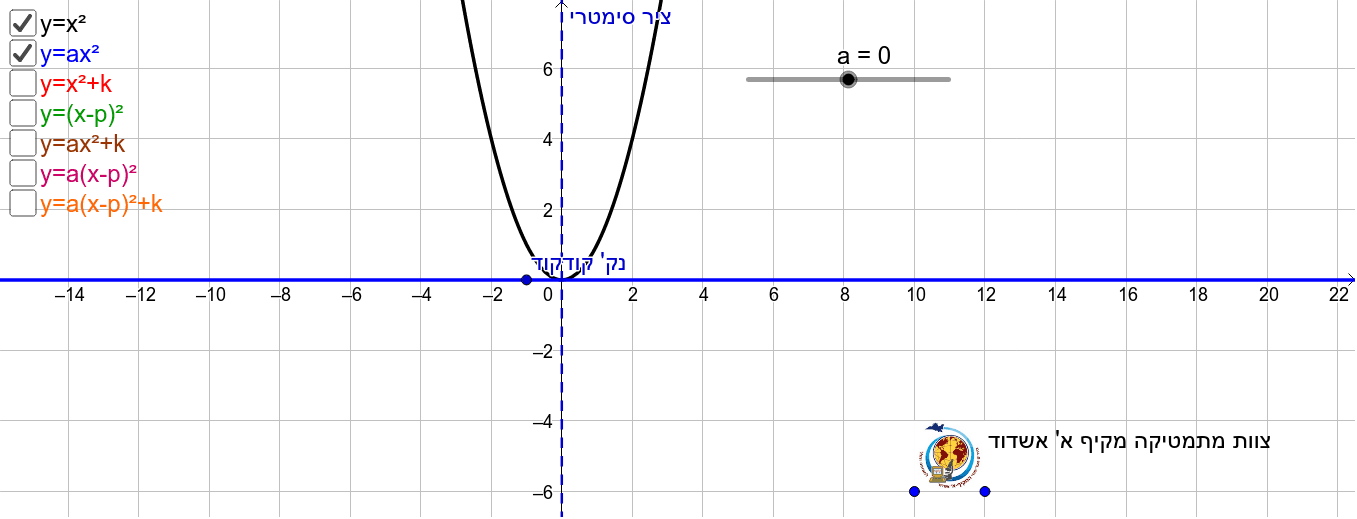



Parabola Y X 2 Geogebra



X Y 2 And X 4 Y 2 Math Central



Solution 1 Graph X 3 1 8 Y 2 2 Write The Coordinates Of The Vertex And The Focus And The Equation Of The Directrix 2 Find All Solution To Each System Of Equations Algerbaiclly




Graphing Questions



Vertex And Intercepts



X Y 2 And X 4 Y 2 Math Central




1 3 Algebra Relationships Between Tables Equations Or Graphs 4 Credits External Ppt Download



Quadratics Graphing Parabolas Sparknotes




Graphing Quadratic Functions Lesson Article Khan Academy



What Is The Graph Of Xy 2 Quora




Graphing Parabolas
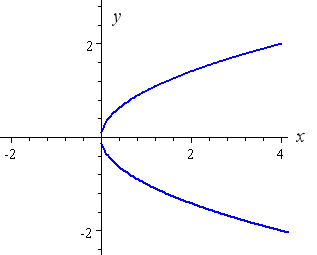



How To Draw Y 2 X 2




How To Draw Y 2 X 2




Parabola X Y 2 Graph Novocom Top




Content Transformations Of The Parabola



1




How To Draw Y 2 X 2



1



Answered Y 3 2 In The Graph To The Right The Bartleby
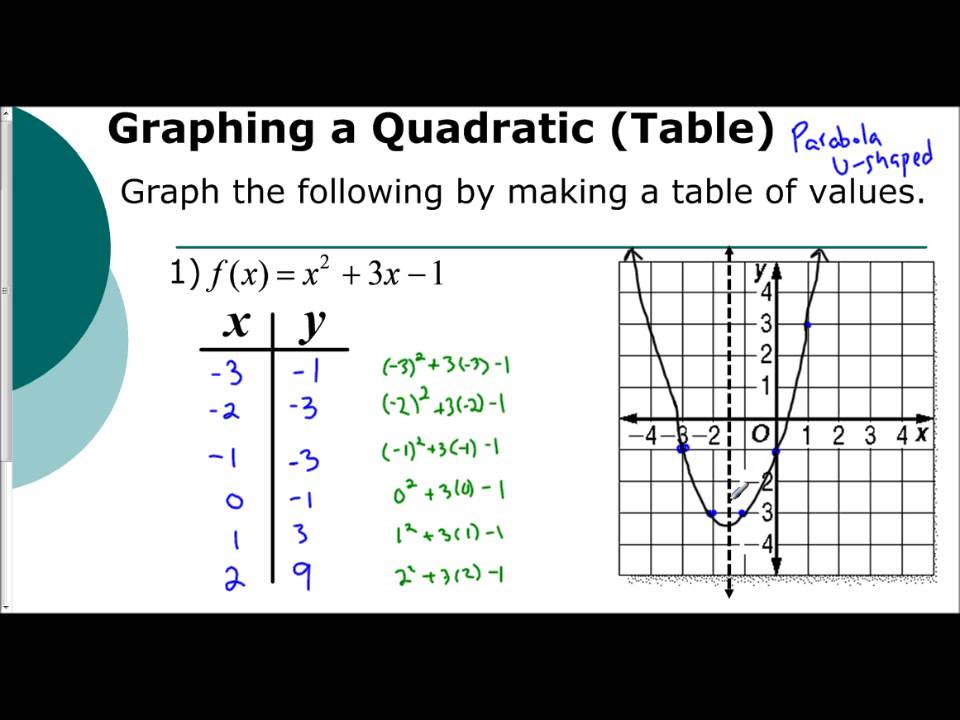



Lesson 5 1 Introduction To Graphing Parabolas Tables Youtube




How To Draw Y 2 X 2



1




Graphing Quadratic Functions Lesson Article Khan Academy




Sketch The Region Enclosed By The Curves Y 2 2x 6 And Y X 1 And Find The Area Youtube
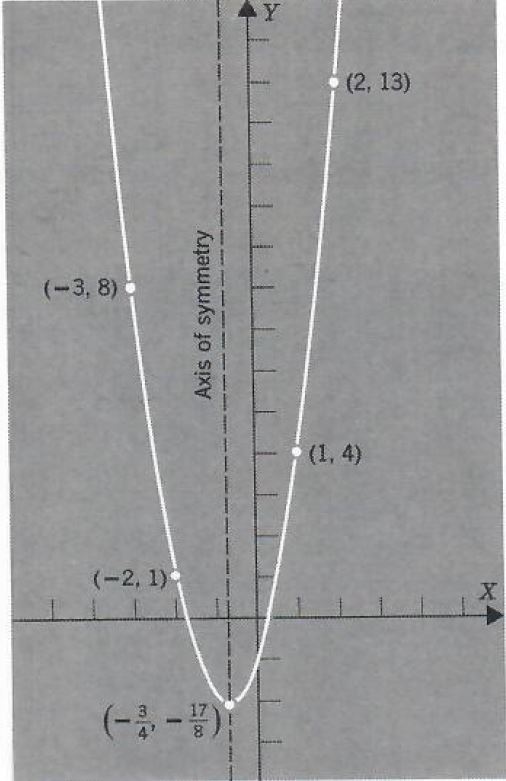



Graph Equation Of Circle And Parabolas Step By Step Math Problem Solver
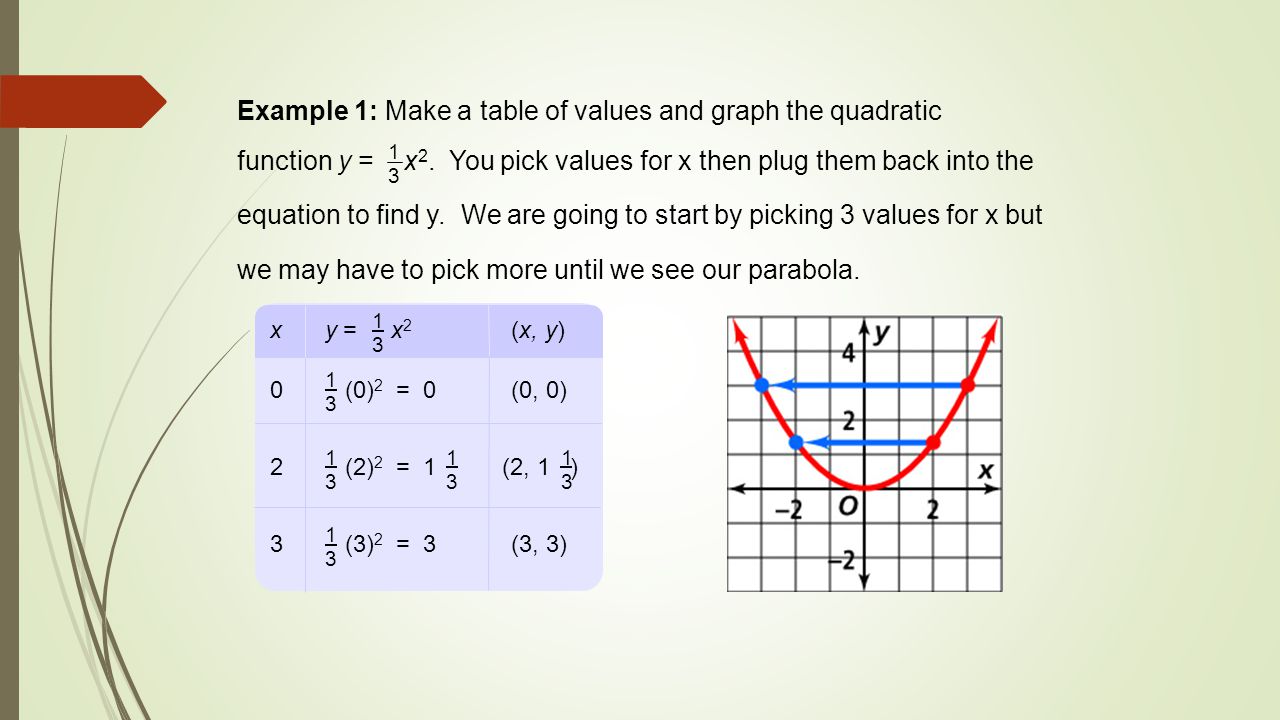



10 1 10 2 Graphing Quadratic Functions By Ms Hall Ppt Download




Plot A Parabola Mapleprimes
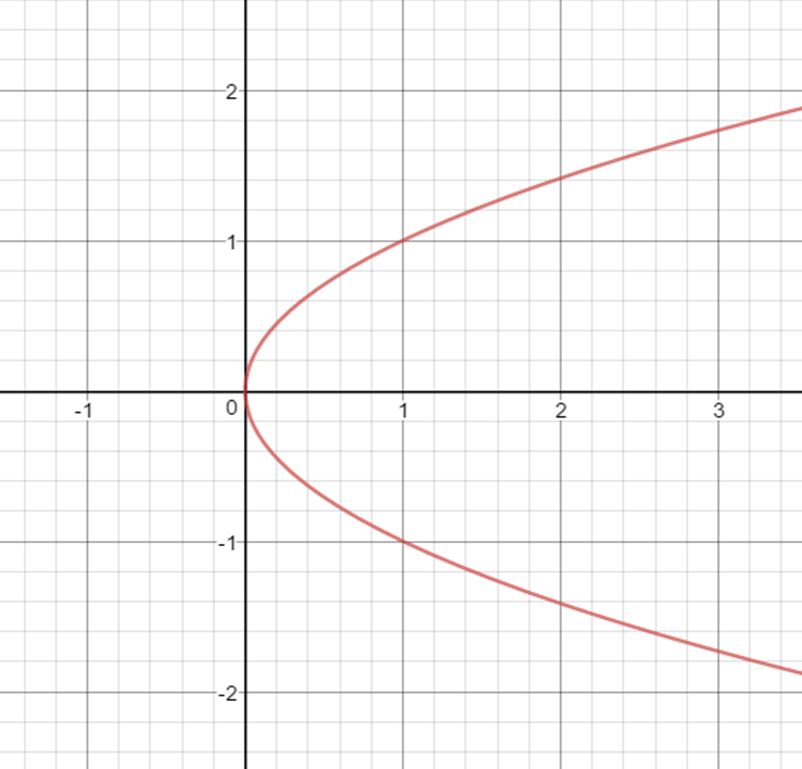



Example Of A Horizontal Parabola X Ay Expii
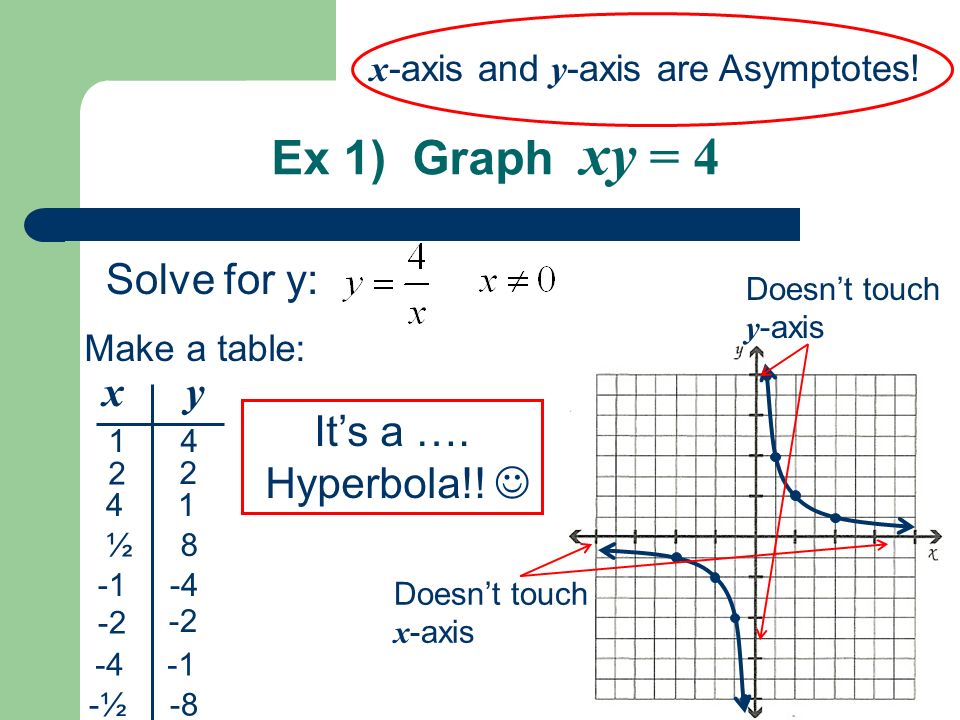



10 1 Identifying The Conics Ex 1 Graph Xy 4 Solve For Y Make A Table Xy Doesn T Touch Y Axis Doesn T Touch X Axis Ppt Download




View Question The Graph Of Y 2x 4 X 4 Is A Parabola In The Xy Plane In Which Of The Following Equivalent Expressions Do The X And Y Coordinates Of
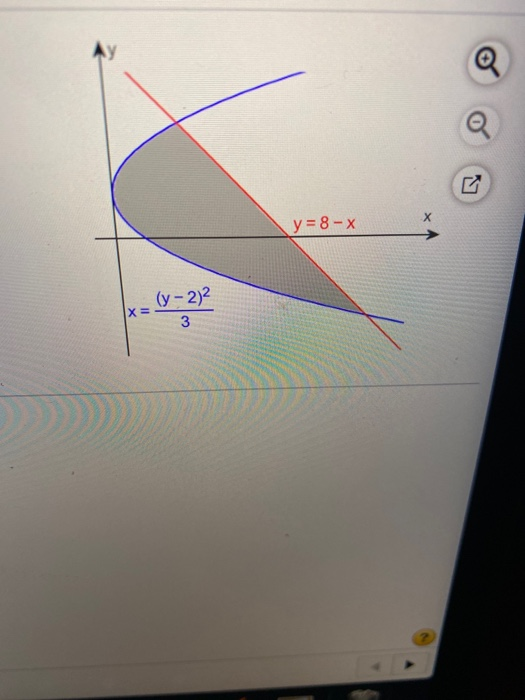



In The Graph To The Right The Equation Of The Chegg Com




Graphing Quadratic Functions Lesson Article Khan Academy




Quadratic Function Wikipedia


